| Day | time | Course | Whats App |
|---|---|---|---|
| Friday | 07.30 – 09.45 | Sys_AD-A March 2026 | https://chat.whatsapp.com/IAfuuVKPfeUDr9MatiuF6T |
| Friday | 13.30 – 15.45 | Sys_AD-D March 2026 | https://chat.whatsapp.com/Ky9ldyaTFoREk3JJPTWeY7 |
| Friday | 10.00-11.20 | Technopreneurship | https://chat.whatsapp.com/CmnP6G9G8F1EeK2nefR6hB |
| Thrusday | 10.15-12.45 | Cloud Computing | https://chat.whatsapp.com/FS1Ja6shzsq7KMWoMx7SNj |
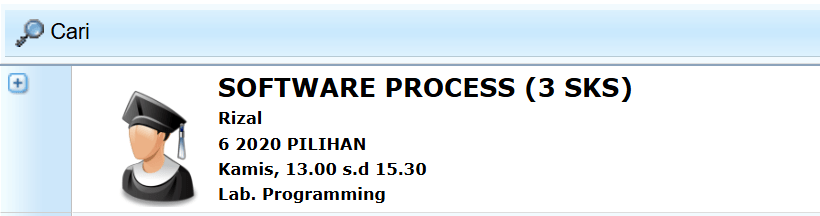
| Thrusday | 13.30-15.45 | Software Process | https://chat.whatsapp.com/JNlmdyqyDMMFyaPWzaI4p1 |
| Thrusday | 8.20-10 | Computer Programming – C | https://chat.whatsapp.com/ESjlxKqr3mI314ivtEhLM9 |
-
-
Class Whats App Groups Fluid Mechanics – B https://chat.whatsapp.com/JB11GSTbloLDI7CTawln0Z Fluid Mechanics – A https://chat.whatsapp.com/IYKgDwkgnfL0g0gfbrlBGc E-Commerce https://chat.whatsapp.com/FWloJ7kk1guIAR3NSJwzm5 Software TEST-Quality https://chat.whatsapp.com/LSJIQTSMh3a0Li9li1dErl Adv. Soft. Eng. https://chat.whatsapp.com/Geye1osiC56KTpIWOuUwzE Data Base – C https://chat.whatsapp.com/FgwnlVPQ16LBv5Np6Tqm7x Data Base – D https://chat.whatsapp.com/EQajSiM5UBVIn6isTg0ptp -
Day Time Course What’s App. Group Friday 7.30-10.00 Sys_AD-A March 2025 https://chat.whatsapp.com/HA6LiI7A9zl5J1n419T9sE Friday 13.30-15.00 Sys_AD-D March 2025 https://chat.whatsapp.com/C581aNpM7mZLpUtacYCo6v Thurs 10.15-12.15 Cloud March 2025 https://chat.whatsapp.com/GGvzZaMwxbX3LGDFKcEFfO Thurs 13.00-15.00 Soft Pro-Ev March 2025 https://chat.whatsapp.com/DlI5MoxMar81D78K3dDaRp Wends 7.30-10.00 DataScience March 2025 https://chat.whatsapp.com/HW5UrJLOBVe7qGplqZ44fV Thurs Forensics March 2025 https://chat.whatsapp.com/BxGnWdOjpKL8NiaMIsdAJi 
-
Day Time Course telegram Comment Tues 10.15-12.45 Advance Soft. Eng https://t.me/+J7NSI4ThYnA5Y2M1 ONLINE Tues 13.00-15.30 Software Quality https://t.me/+XIC_eOms08pkOWQ9 ONLINE Wends 15.30-18.00 E-Commerce ONLINE Thurs 10.15-12.45 X -Plaftom – A https://t.me/+BK1lIkCLvykyMTk1 ONLINE Frid 07.30-10.00 X -Plaftom – B https://t.me/+7-KEe_TV6LhlNmQ1 ONLINE -
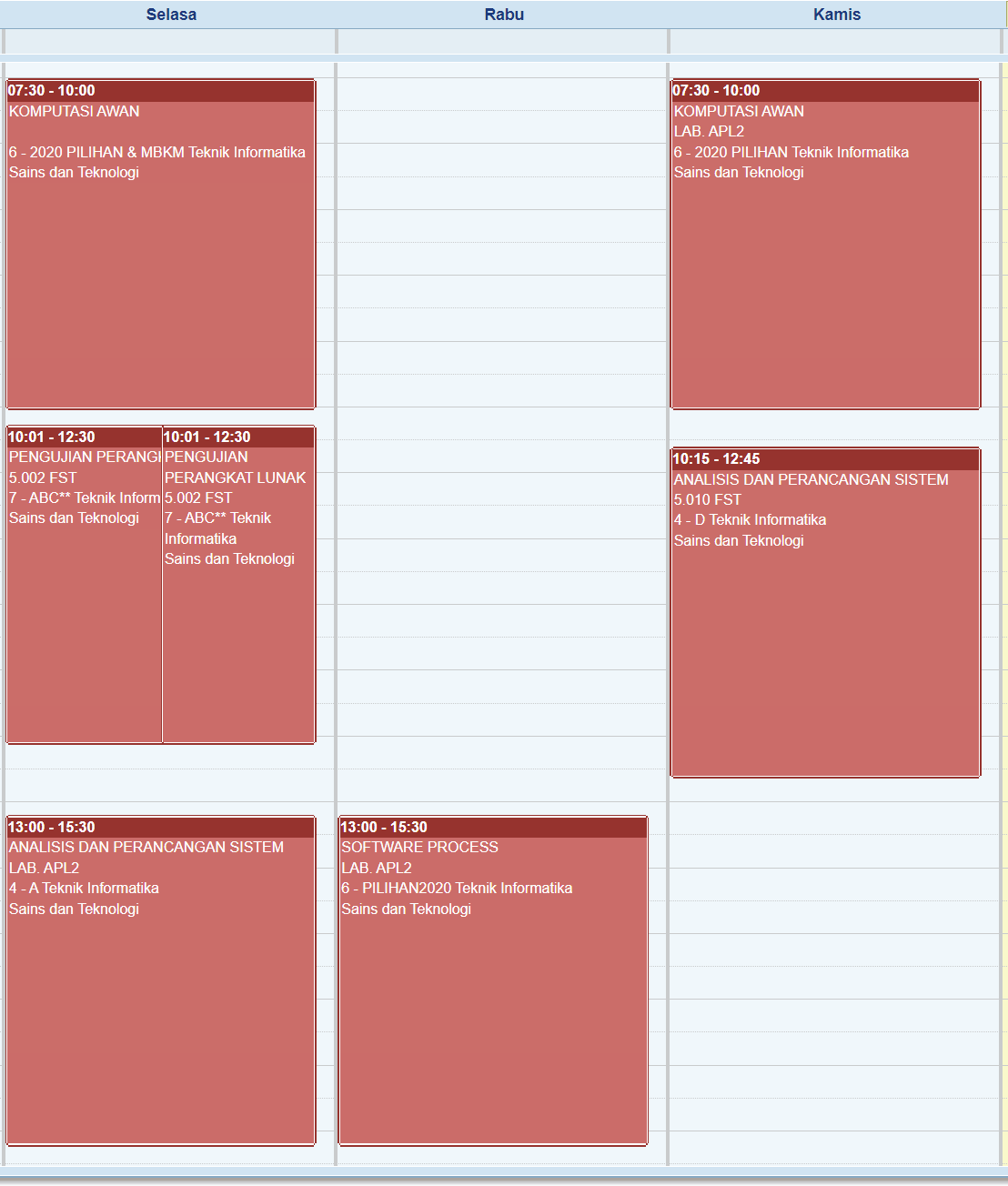
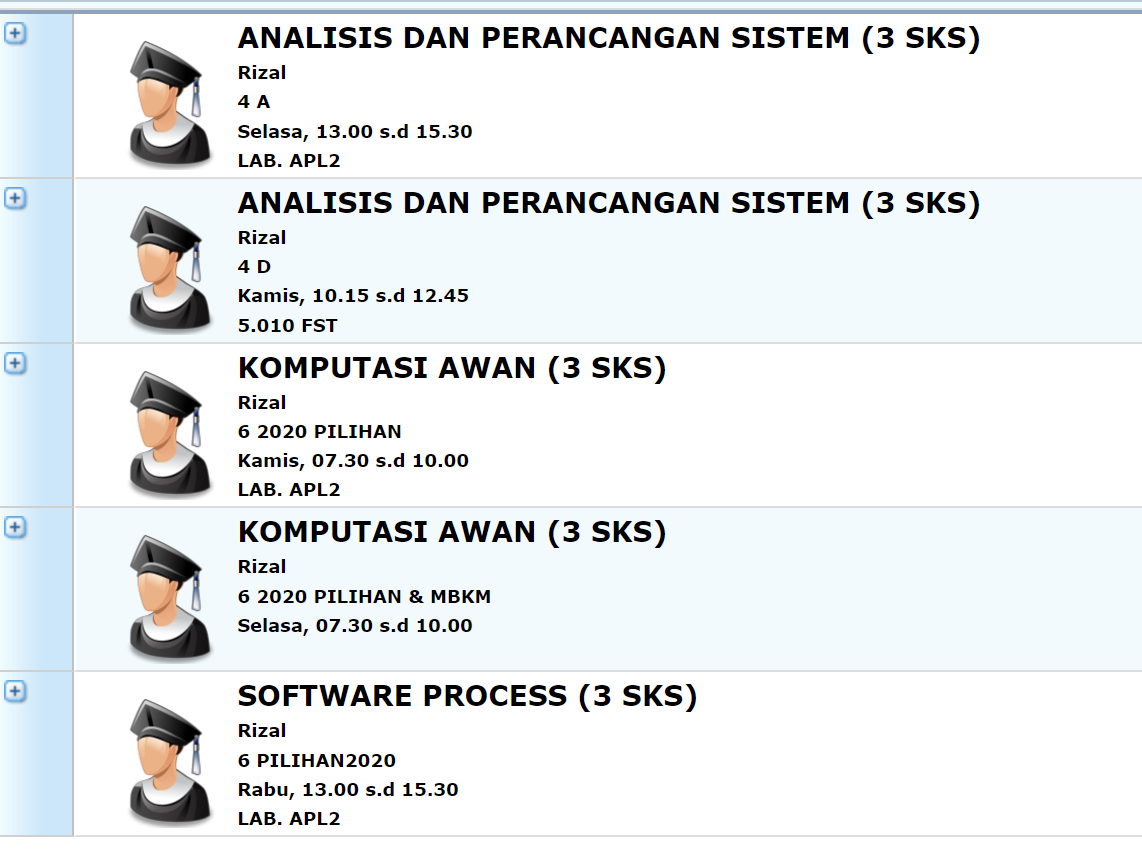
Course Telegram Group GC Noted Analysis and Design [A] https://t.me/+k8hs80mXpH8yYzNl Online Analysis and Design [D] https://t.me/+e96312301v41NTk1 Online Cloud Computing [Tue] https://t.me/+oDe7J0Q2dW80ZTll Online Cloud Computing [Thu ] https://t.me/+oDe7J0Q2dW80ZTll Online Software Process https://t.me/+M8rT39kjAFo1ZWQ1 Online -
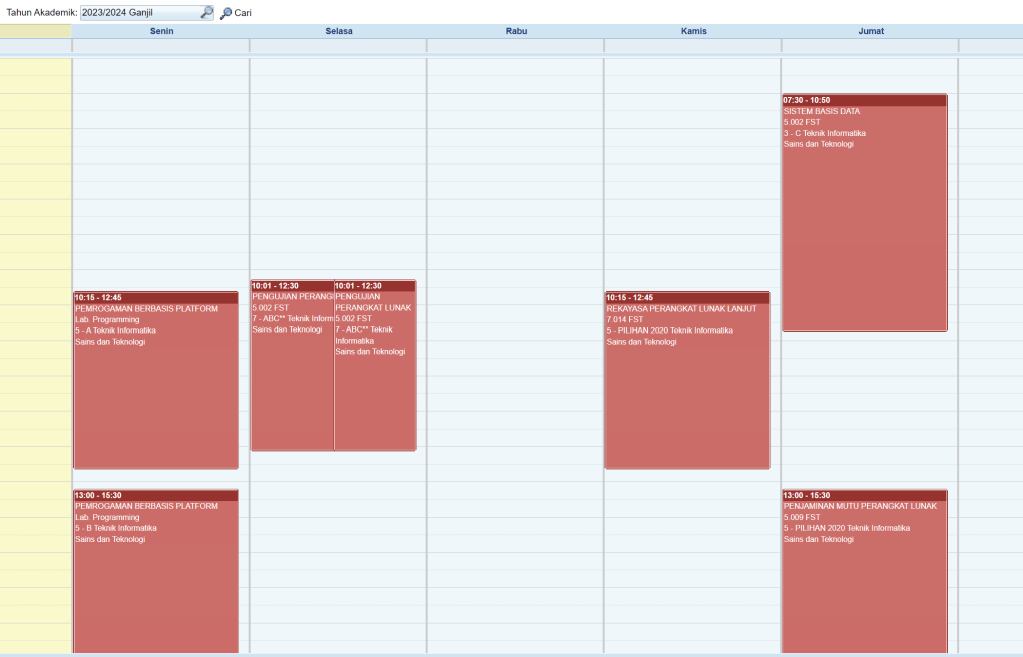
Subject-Class Telegram Groups GC Ms. Teams Note Multi Platform A https://t.me/+PT3XBFvv0OlkMTg1 Multi Platform B https://t.me/+t3YCp9nzY3I3YjM1 Data Base https://t.me/+e_eREwPPXocwZmM1 English Advance Soft. Eng. https://t.me/+MLZywU97ANkzMGZl Software Testing https://t.me/+RVbMOFaTvR1mMjA1 Software Quality https://t.me/+Syjd9GZWh1I5NzVl -

Subject Group Note Computational Intelligence https://t.me/+M_My3zezczYzMTll Software Process https://t.me/+EVyOBP4RSTc4OWZl Elementary Statistics https://t.me/+1xcH8KNtckRkYWJl Cloud Computing https://t.me/+1elQZoBTIm82Nzc1 Untuk CLOUD COMPUTING kerjasama dengan KOMINFO silahkan daftar juga ke : https://digitalent.kominfo.go.id/pelatihan/5666#
-
Monday Tuesday Thursday Course Name Telegram Group 7.30-10.00 Prog. Java (fundamental) https://t.me/+Yb0vFmOOCqcxZjdl 7.30-10.00 Research Methodolgy https://t.me/+j3_vFJVHn600OTJl 7.30-10.00 Artificial Intelligence https://t.me/+WmaO_w59axQ3Zjg1 10.15-12.45 Cloud Computing https://t.me/+Cwz0FRhdAas2ZWFl 10.15-12.45 Soft testing & quality https://t.me/+QozCjRXle2EzMjM1 10.15-12.45 Cloud Computing https://t.me/+Cwz0FRhdAas2ZWFl -
telegram group participant
https://t.me/+m8OgXo3kqtAxNWM9Registrasi : https://www.eventbrite.com/e/rpa-101-tickets-311629049877
-
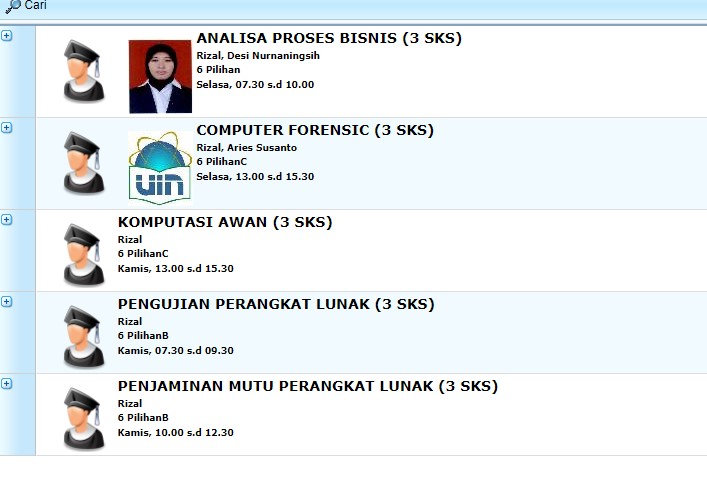
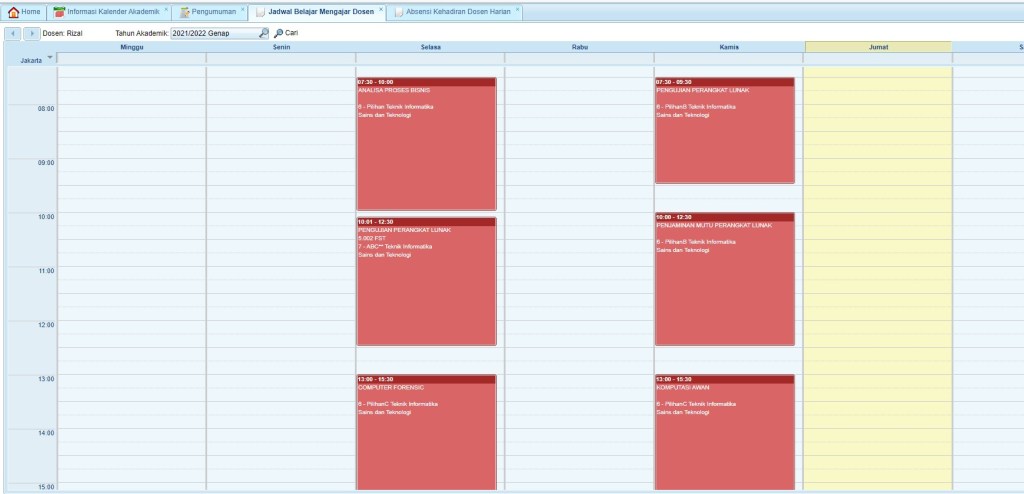
Tuesday Thursday Course Name Telegram Group 7.30-10.00 BPM – Analisa proses Bisnis https://t.me/+rFJS544REhAwZjBl 13.00-15.30 Computer Forensics https://t.me/+ePgT24tTVTlmNWFl 13,00-15,30 Cloud Computing https://t.me/+26K0U876giExNDU1 10.00-12.30 Software Testing [penjaminan mutu Perangkat LUNAK(RPL) dan/atau Kualitas RPL] https://t.me/+KoykXCB8kYo0ZTdl